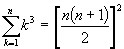Sumatoria y Productoria: 2009

lunes, 4 de mayo de 2009

_Propiedades de la Productoria_

Propieades Multiplicativas:

Demostarción por inducción:

* Tomemos n=1 y veamos si se cumple la Siguient

e igualdad

y la igualdad es cierta para n=1

" La inducción es un razonamiento que permite demostrar una infinidad de proposiciones,dependiendo de un parametreo n que toma una infinidad de valores enteros"

* Supongásmola sierta para n y analicémosla para n+1

( Definición por Inducción)

(Asociatividad de IR)

Luego,

Propiedad Telescópica:

si cada

Demostración por Inducción

Analicemoslo para n=1

Con

y la igualdad es sierta para n=1

* Supongámosla cierta para n y analicémosla para n+1

( definición por inducción)

Luego,

que es lo queríamos demostrar.

Nótese que nuestra exigencia era que para cada k,

.
En particular para

;

. Luego la Simplificación es posible y

lunes, 27 de abril de 2009

_Productoria_

Tambíen conocida como Multiplicatoria o Pitatoria, este es un operador matematico el cual consiste en la multiplicación finita o infinita de factores mediante un simbolo matematico que simplifica la operación, llamado Simbolo Productorio.
Se puede definir como:

$\prod_{k=1}^1 a_k = a_1$

Supuesta definida para un n ≥ 1 fijo, se define

$\prod_{k=1}^{n+1} a_k = (\prod_{k=1}^n a_k)a_{n+1}$

Ejemplos:

Se puede tomar n=1 y aplicar la segunda igualdad para obtener:

$\prod_{k=1}^2 a_k = (\prod_{k=1}^1 a_k)(a_2) = a_1a_2$ .

Definida para n=2, se puede aplicar otra vez la segunda igualdad con n=2 para luego obtener

$\prod_{k=1}^3 a_k = (\prod_{k=1}^2 a_k)(a_3) = (a_1a_2)a_3$ .

Por lo que el producto $\mathit{(a_1a_2)a_3} \,\!$ es el mimso que $\mathit{a_1(a_2a_3)} \,\!$ y, por lo tanto, podemos prescindir del uso de paréntesis sin peligro de confusión y usar simplemente

$\mathit{a_1a_2a_3} \,\!$ para $\prod_{k=1}^3 a_k$ .

Entonces, usar este razonamiento para cualquier $n \in \mathbb{N}$ sin que haya peligro de confusión.
Luego, se puede aplicar la definición de Multiplicatoria, para definir n! (n factorial) como sigue:

$\prod_{k=1}^n k = n!$

Se define 0!=1!=1

lunes, 20 de abril de 2009

_ Propiedades de la Sumatoria_

Entre las propiedades generales de las sumatorias reportadas en la literatura se encuentra las once que se relacionan a continuación, cuya demostración se realiza utilizando el procedimiento matemático de Inducción Completa.

Procedimiento #1:

Procedimiento #2:

Procedimiento #3:

Procedimiento #4:

Procedimiento #5

Procedimiento #6:

Procedimiento #7:

Procedimiento #8:

Procedimiento #9:

Procedimiento #10:

Procedimiento #11:

lunes, 13 de abril de 2009

Sumatoria

La Sumatoria es un tema un tanto difícil de trabajar ya que con todos los elementos de una determinada sucesión.

Por lo cúal para lograr facilitar este trabajo se conviene representar la adición de los términos en forma abreviada mediante el signo ∑ , el cuál se acompaña de una fórmula o término general que define a la sucesión y el rango de valores que se tomará en la variable correspondiente.

"Por lo que esta se entiende como la suma de un finito de números", denotados de la siguiente manera:

Donde:

S: Magnitud resultante de la suma.

T: Cantidad de valores a sumar.

K: Indice de la suma, que va´ría entre h y h+t.

H: Punto inicial de la sumatoria.

H+T: punto final de la sumatoria.

NK: Valor de la magnitud objeto de suma en el punto k.

Donde la notación:

se lee:

Suma de X sub-i (ó sigma sub-i) donde i asume todos los valores de 1 hasta n, ó simplemente suma de X sub-i donde i va de 1 a n.

Las sumatorias se pueden representar bajo dos tipos de notaciones:

* Notación suma abierta: Esta notación va de una representación de sumatoria a cada uno de los elementos que la componen, por ejemplo:

* Notación suma pertinente: Esta notación es al contrario de la suma abierta, va de la representación de cada uno de los elementos de una sumatoria a su representación matemática resumida, por ejemplo: